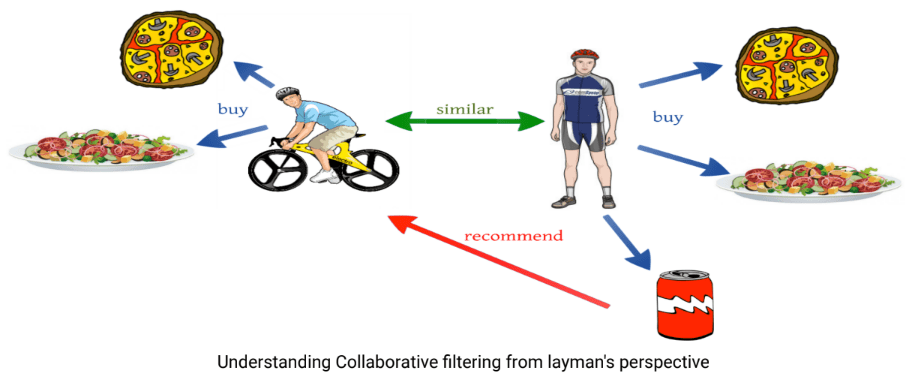
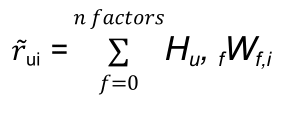×
Get In Touch
We will call or email you ASAP to discuss your project and provide you with a free no obligation quote.
We take privacy seriously. We will never sell your email address to any 3rd party or send you nasty spam.